 Обратное преобразование?
Обратное преобразование?
 |
Наши проекты:
Журнал · Discuz!ML · Wiki · DRKB · Помощь проекту |
|
| ПРАВИЛА | FAQ | Помощь | Поиск | Участники | Календарь | Избранное | RSS |
| [216.73.216.9] |

|
|
| Страницы: (3) 1 [2] 3 все ( Перейти к последнему сообщению ) |
 Обратное преобразование?
Обратное преобразование?
|
Сообщ.
#16
,
|
|
|
|
olegfamus
Можете выложить алгоритм чтения в линейный массив. А то не понятно как правильно читать ваши 20х600? У вас там 2 канала или один? И частота дискретизации какая? |
|
Сообщ.
#17
,
|
|
|
|
Цитата Pavia @ Можете выложить discret = 8000; wFormatTag := WAVE_FORMAT_PCM; nChannels := 1; nSamplesPerSec := discret; wBitsPerSample := 16; nBlockAlign := nChannels * (wBitsPerSample div 8); nAvgBytesPerSec :=nBlockAlign * nSamplesPerSec; |
|
Сообщ.
#18
,
|
|
|
|
Цитата olegfamus @ Результат преобразования Фурье даёт нам спектр исходного сигнала. Мы, по нему можем определить, к примеру, что в звуке нет каких-нибудь частот, которые по идее должны быть, или соотношение энергии гармоник не соответствует ожидаемому. Означает ли это, что у нас некачественно выполнено ПФ? Нет, не означает. Звук мог быть изначально испорчен, и ПФ нам просто это показало.потому как слово нет уж очень похоже на аксиому, что для меня является уж очень узким ответом Можно применить к результату ПФ обратное преобразование и сравнить его с исходным сигналом. Если ОБА преобразования выполнены без ошибок, эти сигналы должны совпадать. На практике, из-за ошибок округления (в основном), эти сигналы будут слегка отличаться. Как правило это отличие за границами слышимости. Поэтом мы и не можем сказать что-либо о качестве ПФ только по обратному преобразованию. |
|
Сообщ.
#19
,
|
|
|
|
Цитата amk @ Как правило это отличие за границами слышимости Возможно, вот в этом я собственно и хотел убедиться лично) Выше мной выложен архив с фразой (типа оригинал), если всё действительно так как вы говорите, я не думаю что выполнить эти перечисленные действия чтобы получить результат займёт для специалиста много времени. Как говориться лучше один раз услышать, чем много раз услышать. |
|
Сообщ.
#20
,
|
|
|
|
Если кому интересно ПРО ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ)
Провёл такой эксперимент: 1. Сделал в программе ширину выборки переменной величиной (от 2 до 250 при частоте дискретизации 8000) Выводы: При обратном преобразовании с различной величиной окна наилучшими в части разборчивости оказался диапазон от 20 до 40 (в общем то интуитивно я так и предполагал), скорее всего ничего нового я здесь не написал, просто ни в одном источнике я не встречал вменяемого обоснования по выбору ширины окна. Кстати при выборке и 2 значения и 250 я тоже различаю смысл сказанного (но тут скорее всего уже начинает влиять способность мозга дополнять пропущенные звуки)… моё субъективное, совершенно дилетантское мнение) 2. Убрал из обратного преобразования фазовый сдвиг, определённый при прямом преобразовании. Выводы: Наличие или отсутствие фазового сдвига при обратном преобразовании совершенно не влияет на конечный результат. Под конечным результатом я понимаю качество услышанного собранного звука. На качество влияет только количество и амплитуды частот в выборке, а не их взаимное расположение на оси времени. Мало этого наилучший результат в качестве сигнала достигается вообще при случайной (Random) начальной фазе. А ели фаза вообще не имеет никакого значения для конечной цели (распознавания звуков) то задача упрощается на порядок по производительности. |
|
Сообщ.
#21
,
|
|
|
|
Цитата olegfamus @ Ну правильно. Ухо человека не воспринимает фазу колебаний, если не во всём диапазоне частот, то в большей его части. Наличие или отсутствие фазового сдвига при обратном преобразовании совершенно не влияет на конечный результат. |
|
Сообщ.
#22
,
|
|
|
|
amk
По поводу уха не знаю. Но суть в том что DCT не содержит фазу и является обратимым. Отличие от FFT оно требует на 1 бит информации в косинусе больше, но при этом отсутствует мнимая составляющая в виде синусов. Другими словами FFT очень избыточен. |
|
Сообщ.
#23
,
|
|
|
|
Цитата Pavia @ Ничуть. При DFT вещественного сигнала отбрасывают старшую половину преобразования, поскольку преобразование симметрично. В результате, на выходе наблюдается в точности то же количество информации, что и после DCT.Другими словами FFT очень избыточен. Но при этом DFT позволяет проще производить манипуляции в частотной области, к примеру, вычислять свёртку или корреляционную функцию. Добавлено Цитата Pavia @ Есть много преобразований, не содержащих фазу, DCT только одно из них. Всё зависит от выбора базисных функций. Некоторые ещё и обходятся без умножений (преобразование Хоара). Вообще, любая вещественная ортонормированная матрица задаёт какое-то преобразование вещественной последовательности (соответственно любая комплексная - комплексной последовательности). суть в том что DCT не содержит фазу и является обратимым Какое-то время много говорили про преобразование Хартли. Но в конце концов оказалось, что оно не сильно и выигрывает у ПФ, а при вычислении свёрток и вовсе ничего не выигрывает. |
|
Сообщ.
#24
,
|
|
|
|
Цитата Pavia @ Другими словами FFT очень избыточен Если я вас правильно понял, то FFT лишь позволяет восстановить исходный сигнал с точностью до бита? для человека же этот набор не является единственным однозначным подтверждением точной копии сигнала? (потому как у той матрицы которую я выложил выше есть бесчисленное количество двойников, отличающихся порядком цифр, и совершенно не отличимых на слух). |
|
Сообщ.
#25
,
|
|
|
|
olegfamus
Если на входе FFT у нас N комплексных чисел, то на выходе N комплексных чисел(2*N действительных чисел). Если на входе FFT у нас N действительных чисел(звук), то на мы можем уменьшить число чисел в 2 раза. Если заменить FFT на DCT, то на мы можем уменьшить число чисел ещё в ~2 раза. Такое преобразование обратимо и без потери информации. Так как такое преобразование выполняется без потерь, то резонно предположить что мозгу безразлична фаза. Однако это надо проверять. Далее идут методы с потерью информации. Если частоты DCT усреднить по схеме MFCC, то на выходе мы имеем 8 чисел на 25 мс. https://www.academia.edu/2519895/Examining_...ion_Performance К сожалению данное исследование не достаточно хорошее. Для кодирования большинства гласных достаточно 2 коэффициентов из 8. |
|
Сообщ.
#26
,
|
|
|
|
Цитата Pavia @ Коргда на входе DFT действительная последовательность, то если N чётно, из N полученных комплексных чисел 2 на самом деле действительные. Остальные разбиваются на пары комплексно-сопряжённых чисел. Это и позволяет уменьшить выход наполовину. Если N нечётно, то действительное число на выходе одно, но остальные тоже делятся на пары комплексно-сопряжённых.Если на входе FFT у нас N комплексных чисел, то на выходе N комплексных чисел(2*N действительных чисел). Если на входе FFT у нас N действительных чисел(звук), то на мы можем уменьшить число чисел в 2 раза. Цитата Pavia @ А вот выход DCT такой избыточностью не обладает. поэтому и сократить ничего нельзя. Вообще в любом обратимом преобразовании так, число выходных действительных величин должно равняться числу входных. Если на выходе больше, то часть из них можно убрать и восстановить по оставшимся.Если заменить FFT на DCT, то на мы можем уменьшить число чисел ещё в ~2 раза. На самом деле DCT и DFT связаны довольно простым соотношением. Поэтому можно сделать DCT и быстренько по нему получить DFT. И наоборот. (На самом деле начало DFT продолженной последовательности в точности равно DCT) |
|
Сообщ.
#27
,
|
|
|
|
Цитата olegfamus @ На качество влияет только количество и амплитуды частот в выборке Тут я похоже маху дал) я пошёл дальше и решил проверить действительно ли разборчивость зависит от амплитуды? как оказалось амплитуду тоже можно исключить из расчётов. Если из спектра выделить определённый диапазон относящийся исключительно к полезному сигналу, а амплитуде присвоить какую нибудь const (например достаточный для прослушивания уровень громкости) - результат будет одинаков с точки зрения распознавания слов Вывод: для распознавания звуков достаточно иметь в наличии только частотные комбинации (при этом эти комбинации не должны зависеть от мужского женского или детского тембра - думаю это уже отдельная тема), что ещё более упрощает задачу с производительностью) зы: выводы я пишу скорее всего для себя, а не в качестве аксиомы для остальных исследователей. Просто мне интересна реакция профессиональных специалистов на такие утверждения. Возможно я что то упустил в своих параметрах и такие результаты получились у меня случайно) возможно математика всё объяснит, как это было с фазой? |
|
Сообщ.
#28
,
|
|
|
|
olegfamus
Амплитуда нужна для поиска локального максимума. Можно сделать локальную бинаризацию. Берём окно 25 мс удаляет постоянную составляющую, затем переводим в частоты находим среднее и используем в качестве порога: всё что выше среднего 1 всё что ниже 0. Цитата olegfamus @ математика всё объяснит, как это было с фазой? Вы неправильно понимаете суть математики. Математика работает в рамках своих аксиом. А вот какие формулы можно или нельзя использовать в качестве аксиома определяет природа вещей, естество. Для этого и нужны учёные что-бы вот в таких вот задачах находить формулы. Для примера можете построить треугольник с гепотинузой 10 см. Можете. А найти площадь при опущенной на неё высоте в 6 см. Тоже можете. Площадь равна половине произведения основания на высоту. S=1/2*c*h. Однако естество прямоугольного треугольника запрещает использовать h>5 см. Другими словами какие законы включать или выключать определяет естество. Или какими формулами можно пользоваться, а какими нельзя. Тут хорошо что естество выводится. Однако в прикладных областях включая распознавание звука это не выводится. А экспериментально обосновывается из сходя из гипотез учёных. Цитата amk @ А вот выход DCT такой избыточностью не обладает. поэтому и сократить ничего нельзя. Вообще в любом обратимом преобразовании так, число выходных действительных величин должно равняться числу входных. Если на выходе больше, то часть из них можно убрать и восстановить по оставшимся. Ваше утверждение ложное. Рассмотрит симметричные вейвлеты Добиши. |
|
Сообщ.
#29
,
|
|
|
|
Цитата Pavia @ удаляет постоянную составляющую А какой способ вы имеете в виду? хочу проверить рекомендацию |
|
Сообщ.
#30
,
|
|
|
|
olegfamus
Цитата olegfamus @ А какой способ вы имеете в виду? хочу проверить рекомендацию Есть два алгоритма. 1. Во временной области рассчитываете среднее и вычитаете из сигнала. 2. Фильтр высоких частот, т.е высокие пропускаем низкие обособляем. В статьях видел рекомендацию частотой среза в 1 КГц (как-то много). Думаю спуск(крутизна фильтра) должен быть пологим. Ищите онлайн калькулятор фильтра там списываете коэффициенты и подставляете их в КИХ (FIR) фильтр. Лично я пока играюсь с Гаусовым фильтром у меня лучший результат сглаживание по 150 отсчётов на fd=8000. На звукоформе после ФНЧ видны усиления и ослабления сигнала. Смыкания и размыкания губ? Они тоже не влияют. 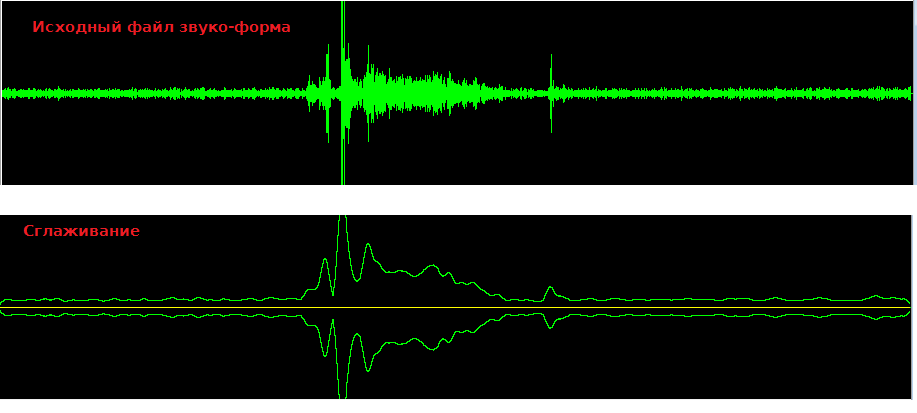 Основная цель убрать эффект растекания спектра(Имени кого не помню) который возникает из-за того что правый конец сигнала не совпадает с левым по амплитуде. Получается ступенька, а она имеет спектр вида Sinc(f) в частотной области. Короче из-за того что частота исходного сигнала не совпадает с периодом DFT получаем пик/горку вблизи 0 частот. Вот его надо убрать. Вычитание среднего отлично с этим справляется. 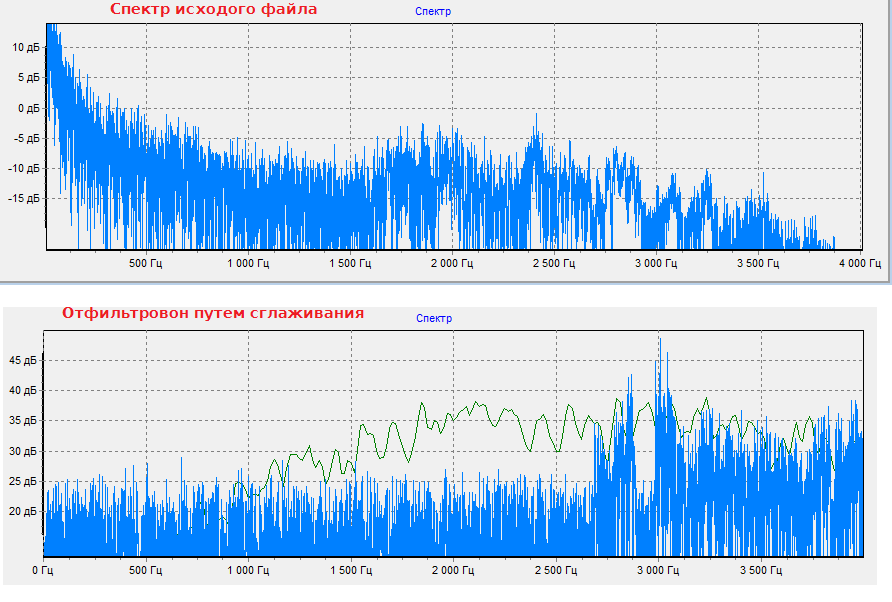 |
0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)
0 пользователей:
[ Script execution time: 5,4227 ] [ 15 queries used ] [ Generated: 1.02.26, 22:56 GMT ]



