Определения x y координат по оси z

[cpp_and_asm]

Всем привет. Вопрос скорее всего простой чем сложный.
Хочу понять как определяется координаты X и Y на экране компьютера когда у нас три оси X,Y,Z, Попробую правильно сформулировать вопрос.
У нас есть точка point(x,y,z), но на мониторе то есть координаты только x и y, и выходит что когда мы будем ставить точку point(x,y,z), мы должны рассчитать точку x и y.

Вот как я понимаю из познаний геометрии. в двумерном пространстве мы имеем одну плоскость, xy. А в трехмерном пространстве 3 плоскости, xy, xz, yz
Как мне получается с ними работать?

То есть просто нарисовать 2 точки в 3D, Вообще куда смотреть ? Подскажите направления.

[MBo]

>Вообще куда смотреть ?

На понятие проекции

[cpp_and_asm]

А можно ссылку на материал пожалуйста

Добавлено 17.09.14, 10:08
Собственно с векторами я знаком, я понимаю что такое проекция вектора на координатной оси, но только на двумерной. Вот нужно с трехмерной разобраться и попробовать хоть куб нарисовать что бы вертелся

[MBo]

http://www.intuit.ru/studies/courses/70/70/lecture/2104
простейшая проекция - ортографическая на плоскость xy (Z=0) - при отрисовке точек просто не учитывается Z-координата

Сообщение отредактировано: MBo - 17.09.14, 10:15

[cpp_and_asm]

Мне сейчас это подойдет. Надо найти с примерами. Что бы на бумаге сделать можно было

[cpp_and_asm]

Вообще сложновато. Есть ли какой нибудь учебник что ли, что бы с примерами на практике.

[amk]

Цитата MBo @ 17.09.14, 10:12

простейшая проекция - ортографическая на плоскость xy (Z=0) - при отрисовке точек просто не учитывается Z-координата

В OpenGL и DirectX именно она и реализована. Правда перед ней как правило производится поворот и, часто, перспективное преобразование. Координата z используется для определения видимости точки (посредством z-буфера).

[cpp_and_asm]

Всем привет, начал изучать, и вот уже рисую свой первый треугольник. И возникло непонимание. Сейчас опишу
Я уже понял, что можно представить камеру в виде точки, а то куда она смотрит в виде плоскости на которую нужно проецировать изображения.
Так как система координат монитора начинается с верхнего левого угла, мы должны ее переделать в 3D координаты, и что бы центр был по середине экрана.
Вот код который рисует на экране треугольник:

    // Заполняю координаты точек треугольника
    treangle t;
    t.setA(-15,-15,1);
    t.setB(15,15,1);
    t.setC(15,-15,1);
 
    qreal dist = 5; // дистанция от камеры
    qreal x,y;
 
    // X и Y для точки А (красного цвета)
    x =  xSize/2 + t.A[0]   *  dist / (t.A[2]+dist);
    y =  ySize/2 - t.A[1]   *  dist / (t.A[2]+dist);
 
    vertexTriangle[0].setX(x);
    vertexTriangle[0].setY(y);
 
    // X и Y для точки B (Зеленого цвета)
    x =  xSize/2 + t.B[0]   *  dist / (t.B[2]+dist);
    y =  ySize/2 - t.B[1]   *  dist / (t.B[2]+dist);
 
    vertexTriangle[1].setX(x);
    vertexTriangle[1].setY(y);
 
    // X и Y для точки С (Синего цвета)
    x =  xSize/2 + t.C[0]   *  dist / (t.C[2]+dist);
    y =  ySize/2 - t.C[1]   *  dist / (t.C[2]+dist);
 
    vertexTriangle[2].setX(x);
    vertexTriangle[2].setY(y);

А вот результат: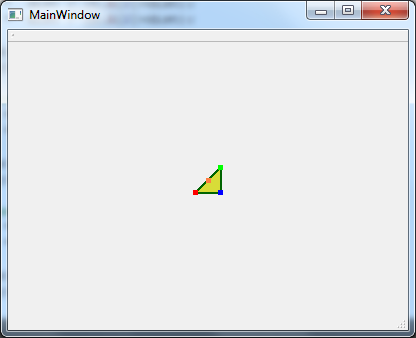


На картинке мы видим треугольник
Оранжевая точка это середина координат (0,0,0)
Вершина треугольника A - Красная точка
Вершина треугольника B - Зеленая точка
Вершина треугольника C - Синяя точка

Теперь о моем расчете:
Вот расчет для точки А
x = xSize/2 + t.A[0] * dist / (t.A[2]+dist);
y = ySize/2 - t.A[1] * dist / (t.A[2]+dist);

xSize/2 и ySize/2 Делим Ширину и высоту экрана на 2 что бы получить центр окна
Теперь: t.A[0] * dist и t.A[1] * dist
dist - это дистанция камеры по оси z То есть умножая на точку мы как бы делаем приближения и удаления камеры по оси OZ
(t.A[2]+dist) это соответственно z+dist

Теперь вопрос!
Как бы я не менял dist (Дистанцию камеры по оси oz) она меняется как попало!
Тоесть формулу я не правильно понял!

Можете объяснить как будет правильно?

[OpenGL]

Что значит "как попало"?

[cpp_and_asm]

Это значит что разницы dist = 5 и dist = 50 практически нет

[Pavia]

cpp_and_asm
С английским как у вас? Просто на английском можно подобрать материал более разжёванный.
Второе вам надо освежить свои знание о математике и геометрии.
Прочитать про матрицы и их преобразования. И про системы отсчёта.

Грм. Код читать ваш невозможно. Его надо писать так, чтобы было понятно без комментариев.
Вместо A,B,C надо писать
PointA, PointB,PointC или
Points[0], Points[1], Points[2]
Вместо [0], [1], [2] надо писать x,y,z.

Цитата cpp_and_asm @ 19.09.14, 08:39

Теперь вопрос!
Как бы я не менял dist (Дистанцию камеры по оси oz) она меняется как попало!
Тоесть формулу я не правильно понял!

Можете объяснить как будет правильно?

Формулы вроде правильные. Дистанция это не камера это фокус камеры, хотя при моделирование обычно одно и тоже. У вас положение точек очень близко к проекционной плоскости отнесите её подальше не на 1, а на 100. И меняйте дистанцию от фокуса камеры до проекционной плоскости несильно.

Что-бы упростить подбор этих параметров параметры камеры задают при помощи ближней и дальней плоскости отсечения и угла обзора камеры.
А ещё чтобы упростить расчёт этих параметров их вовсе не рассчитывают, а настраивают в графическом редакторе, а после сохраняют и копируют.
Хотя для эффектов движения камеры, прицеливания их всё же приходится рассчитывать.

Добавлено 19.09.14, 09:45

Цитата cpp_and_asm @ 19.09.14, 09:32

Это значит что разницы dist = 5 и dist = 50 практически нет

по пробуй менять как dist = 10/i; где i некоторый параметр от 1 до 100.

[cpp_and_asm]

Цитата

С английским как у вас? Просто на английском можно подобрать материал более разжёванный.

Плохо.

Цитата

Второе вам надо освежить свои знание о математике и геометрии.
Прочитать про матрицы и их преобразования. И про системы отсчёта.

Спасибо за совет, но прежде чем перейти к матрицам, я должен понять что будет значить каждый элемент матрицы.
Именно по этому я начинаю с мелкого. Так что прошу помощи разобраться тут!

Цитата

Грм. Код читать ваш невозможно. Его надо писать так, чтобы было понятно без комментариев.
Вместо A,B,C надо писать
PointA, PointB,PointC или
Points[0], Points[1], Points[2]
Вместо [0], [1], [2] надо писать x,y,z.

Да))) Я изначально именно так и сделал! Но подумал что вам будет не ясно.
Сейчас сделал вот такой вариант кода. Оцените, в таком формате будет яснее?

    qreal vertex[3][3] = {
                            {-15,-15,100}, {15,15,100}, { 15,-15,100} ,
                         };
 
    for (int i=0; i < 3; i++)
    {
        // Проецирование X и Y точки на плоскость с учетом Z
        qreal x =  xSize/2 + vertex[i][0]   *  dist / (vertex[i][2]+dist);
        qreal y =  ySize/2 - vertex[i][1]   *  dist / (vertex[i][2]+dist);
        vertexTriangle[i].setX(x);
        vertexTriangle[i].setY(y);
    }

Цитата

Формулы вроде правильные. Дистанция это не камера это фокус камеры, хотя при моделирование обычно одно и тоже. У вас положение точек очень близко к проекционной плоскости отнесите её подальше не на 1, а на 100. И меняйте дистанцию от фокуса камеры до проекционной плоскости несильно.

А теперь результат со скринами

Скрытый текст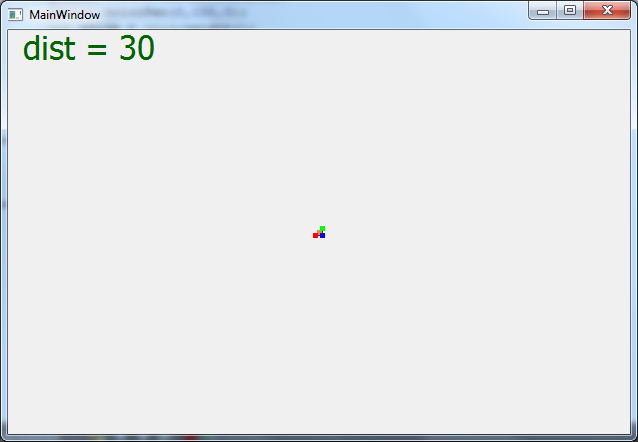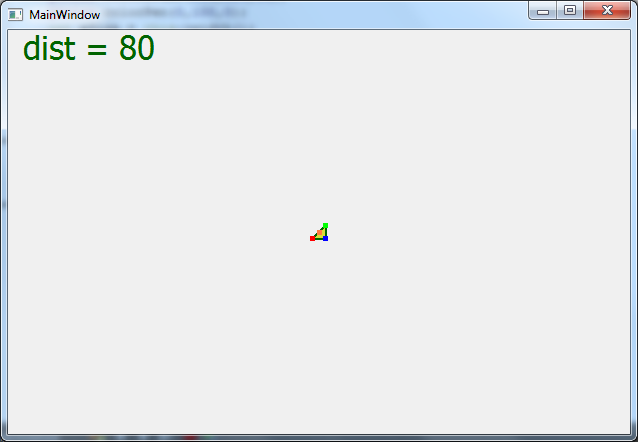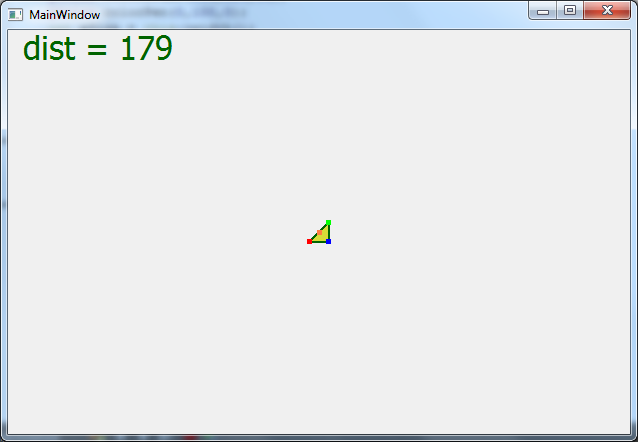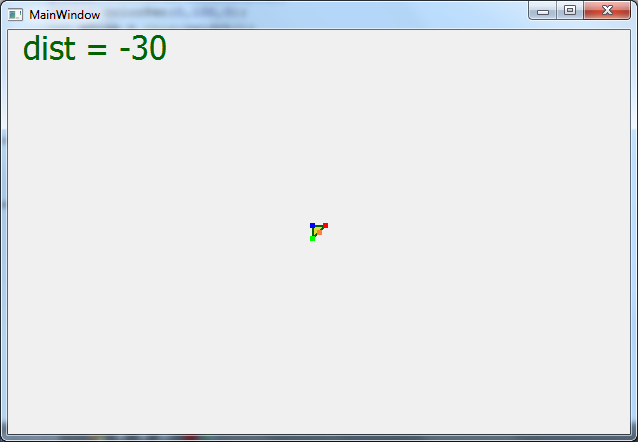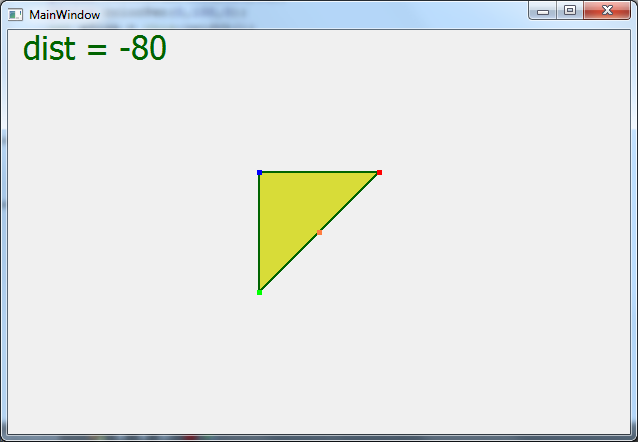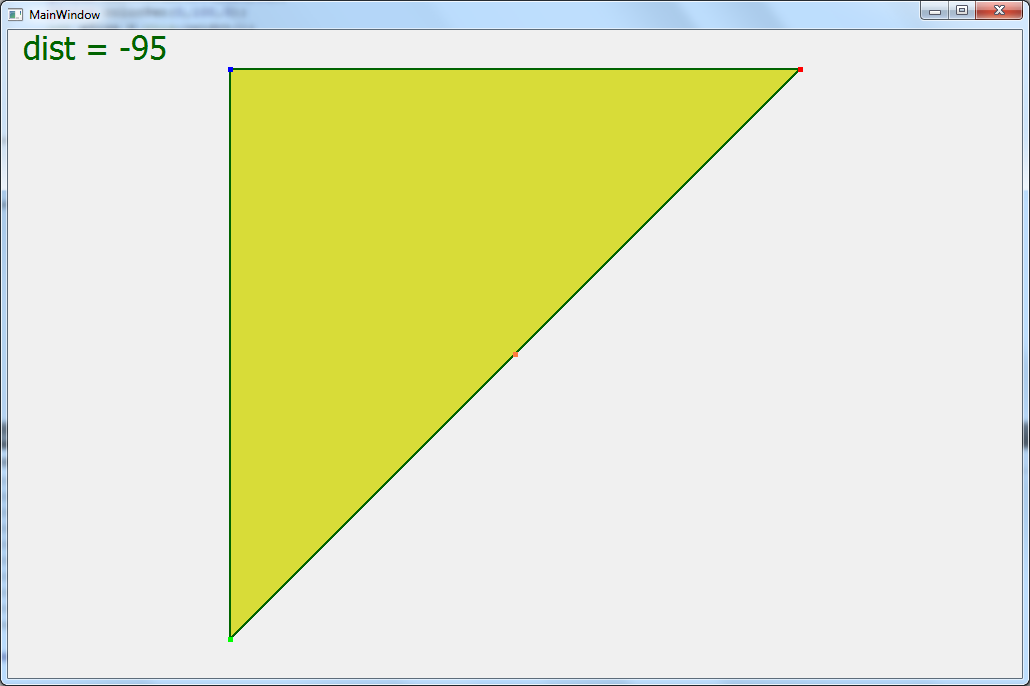

Если обратить внимание, то когда dict отрицательна то треугольник увеличивается и уменьшается как нужно, но система координат перевернута

Добавлено 19.09.14, 10:13

Цитата

по пробуй менять как dist = 10/i; где i некоторый параметр от 1 до 100.

Не видно треугольника, он будто очень далеко

Добавлено 19.09.14, 10:39
Уф! Долго рисовав на листке я понял!

    qreal vertex[3][3] = {
                            {-15,-15,100}, {15,15,100}, { 15,-15,100} ,
                         };
 
 
    for (int i=0; i < 3; i++)
    {
        // Проецирование X и Y точки на плоскость с учетом Z
        qreal x =  xSize/2 + vertex[i][0]   *  vertex[i][2] / dist;
        qreal y =  ySize/2 - vertex[i][1]   *  vertex[i][2] / dist;
        vertexTriangle[i].setX(x);
        vertexTriangle[i].setY(y);
    }

Я должен Z делит на дистанцию, а не наоборот..

Добавлено 19.09.14, 10:40
Теперь можно и к матрицам преглядываться

Добавлено 19.09.14, 10:57
тоже не верно, поторапился

Сообщение отредактировано: cpp_and_asm - 19.09.14, 10:57

[Pavia]

Перспектива

Задача нужно найти формулу перевода координат точки * на плоскость при помощи перспективного проецирования.
Напоминаю что в одноточечной перспективной проекции все линии идут в общую точку называемой фокусом.

Y
^
|               h2
|               /|
|              / |
|             /  |
|            /   |
|           /    |
|          /     |
|         /      |
|      h1/       |
|       /|      /|
|      / |  y*/  |
|     /  |  /|   |
|    / y'|/  |   |
|   /   /|   |   |
|  /  /  |   |   |
| / /    |   |   |
|//      |   |   |
+--------+---+---+--->Z
E        N   Z   F

Дано:
E - фокус
N - плоскость проекции или экран или ближняя стенка мира. Будем считать, что Z в этой точке равен 0.
F - дальняя стенка мира
* - точка на которую мы смотрим
y - реальное положение точки * по оси Y
y' - проекционное положение точки * на экране
Z - реальное положение точки * по оси Z
Найти формулу T такая что y'=T(y,z) и x'=T(x,z)

Решение:

Треугольники (Ey'S) (EyZ) пропорциональны. Откуда выпишим формулу соотношения сторон 1)
1)y'/y=EN/EZ
Найдем проекционную кординату y'
2)y'=y*EN/EZ
Упростим
3)y'=y*(N-E)/(Z-E)
4)y'=y*(0-E)/(Z-E)
Для x аналогично
5) x'=x*(-E)/(Z-E)
Иногда -E заменяют на D
6) x'=x*D/(Z+D)

Так что формулы в 8 сообщение корректные.

А то что при увеличении Distance кортика увеличивается так это нормально. Вы просто увеличиваете фокус, а камера стоит на месте. А вот если вы камеру будете относить, то расстояние до объекта от плоскости проекции будет меняться в сторону увеличения. А вот размер объекта будет уменьшаться.

Сообщение отредактировано: Pavia - 20.09.14, 08:06

[cpp_and_asm]

Тогда нужно переходить к матричным преобразованиям. В принципе понятно..

[amk]

Цитата cpp_and_asm @ 19.09.14, 10:09

ежде чем перейти к матрицам, я должен понять что будет значить каждый элемент матрицы.

На самом деле, если в задаче появляется матрица, то обычно отдельные элементы этой матрицы самостоятельного значения не имеют. Иначе бывает как правило в специально подобранных, искусственных примерах. В большинстве задач и в машинной графике в частности, можно выбрать некоторый набор особенных матриц, посредством манипуляций с которыми получаются все остальные матрицы. В машинной графике такими матрицами являются матрицы поворота объектов и камеры, матрицы переноса, матрицы растяжений, матрица перспективного преобразования. Большинство их этих матриц формируются в разных процедурах настройки сцены и сразу пускаются в дело, но знать о них, пожалуй, полезно - проще разбираться, что происходит, так сказать, за кадром, в недрах графической библиотеки.

[Axis]

Вообще я бы посоветовал прочитать книгу (а точнее 2 или 3 главы этому посвящены): Математические основы машинной графики. Роджерс Д., Адамс Дж.
Лучше ничего не видел, рассказано всё на пальцах, с графиками, сразу всё понятно становится. Не рассмотрено применение кватернионов, но на данном этапе они и не нужны. Видел и другие книги, статьи, но всё же эту книгу считаю лучшей. Потратил часа 3, разобрался без проблем, в последствии для тренировки реализовал простенький софтварный 3д рендер.

[Pavia]

Axis
Наконец-то дошел до вашей книге. Ну что же отличная книга. Лично я больше привык к
"Ф.Хилл OpenGL. Программирование компьютерной графики.djvu" - там матриц меньше зато на сплайны больше уклон сделан.
Правда в обоих этих книгах много чего не хватает.
В этом плане 3-х томник более полон:
Graphics_Gems_1,ed_A.Glassner.pdf
Graphics_Gems_2,ed_J.Arvo.pdf
Graphics_Gems_3,ed_D.Kirk.pdf
хотя сейчас стоит ещё расширить одним или двумя томами.

Хочу ещё добавить математика математикой, но мне больше нравится как описано более живым языком в DirectX SDK
http://msdn.microsoft.com/en-us/library/wi...6(v=vs.85).aspx
http://msdn.microsoft.com/en-us/library/wi...9(v=vs.85).aspx

[Axis]

Ну если задача понять проецирование, то поняв назначение матриц (что внутри не важно, API выдают готовые матрицы) всё будет пониматься элементарно. Раньше для меня сделать свободную камеру было магией, после прочтения сел и сделал. Теорию в любом случае знать надо. А вот Graphics_Gems не глядел, надо взглянуть.