аппроксимация экспонентой f(x)=a*exp(b*x)+c

Здравствуйте.
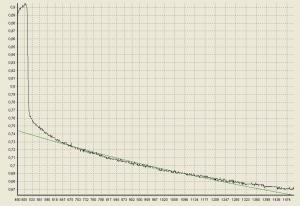
Подскажите пожалуйста каким способом лучше всего произвести аппроксимацию данных экспонентой f(x)=a*exp(b*x)+c.
Исходные данные: набор из 1000 точек с интервалом 50мкс.
Пробовал ввести данные по ссылке http://twtmas.mpei.ac.ru/mas/worksheets/Fit_f_x_a_b_c.mcd).
Брал не все точки, а только 20 с равным интервалом - получилось красиво.
Но какой метод там используется так и не нашел.
Спасибо.

SumX := 0;
SumY := 0;
SumSqrX := 0;
SumXY := 0;

for i := 1 to Nuz do //до число узлов (точек)
begin
SumX := SumX + X[i];
SumY := SumY + ln(Y[i]);
SumSqrX := SumSqrX + Sqr(X[i]);
SumXY := SumXY + X[i]*ln(Y[i]);
end;

b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX));
a := (SumY-b*SumX)/Nuz;
b1 := b;
a1 := exp(a);

Y_calc := a1*exp(b1*X);//интерполяция

Просто линеаризация
Если коэфф "С" для Вас критично - задавайтесь им предварительно, и вместо y[i] будет y[i]-c или плюс (сами разберетесь...)

Сообщение отредактировано: repz - 17.12.09, 07:33

Просто линеаризацию я уже пробовал. Получается не совсем то что хотелось бы - см. рисунок.

Прикреплённая картинка

Линеаризация - это не аппроксимация линейной функцией

Выложите свои "Точки" (таблично), посмотрим что получается...

Цитата

Линеаризация - это не аппроксимация линейной функцией

Это все понятно. Пробовал сделать аппроксимацию функцией f(x)=a*exp(b*x)+c. Коэффициент с принял за константу, перенес влево, логарифмировал и т.д. и т.п. Тоже самое что вы предлагали. Ваш код и мой дали один и тот же результат (что в принципе логично).

Точки (шаг по X равный):
-0,897
-0,891
-0,876
-0,854
-0,822
-0,795
-0,778
-0,771
-0,766
-0,765
-0,763
-0,762
-0,762
-0,763
-0,76
-0,76
-0,76
-0,76
-0,76
-0,757
-0,757
-0,757
-0,756
-0,754
-0,756
-0,754
-0,754
-0,754
-0,754
-0,753
-0,753
-0,753
-0,751
-0,753
-0,751
-0,75
-0,75
-0,75
-0,75
-0,75
-0,75
-0,75
-0,748
-0,748
-0,748
-0,75
-0,748
-0,747
-0,748
-0,748
-0,745
-0,747
-0,747
-0,747
-0,747
-0,747
-0,744
-0,745
-0,747
-0,744
-0,744
-0,744
-0,744
-0,744
-0,742
-0,742
-0,741
-0,742
-0,742
-0,741
-0,741
-0,742
-0,741
-0,741
-0,741
-0,741
-0,739
-0,739
-0,739
-0,738
-0,739
-0,739
-0,738
-0,738
-0,738
-0,738
-0,736
-0,736
-0,739
-0,738
-0,736
-0,736
-0,738
-0,736
-0,736
-0,736
-0,736
-0,735
-0,735
-0,735
-0,735
-0,735
-0,735
-0,735
-0,733
-0,733
-0,733
-0,733
-0,732
-0,733
-0,732
-0,733
-0,733
-0,733
-0,733
-0,73
-0,732
-0,732
-0,733
-0,733
-0,732
-0,732
-0,73
-0,73
-0,73
-0,73
-0,73
-0,729
-0,729
-0,729
-0,729
-0,73
-0,729
-0,729
-0,729
-0,727
-0,729
-0,729
-0,729
-0,727
-0,727
-0,729
-0,729
-0,729
-0,729
-0,729
-0,729
-0,727
-0,727
-0,727
-0,726
-0,726
-0,726
-0,727
-0,724
-0,726
-0,726
-0,726
-0,726
-0,726
-0,726
-0,726
-0,724
-0,729
-0,724
-0,724
-0,724
-0,723
-0,724
-0,724
-0,724
-0,724
-0,724
-0,724
-0,723
-0,723
-0,723
-0,723
-0,723
-0,721
-0,723
-0,723
-0,723
-0,723
-0,723
-0,723
-0,721
-0,721
-0,723
-0,721
-0,721
-0,721
-0,721
-0,721
-0,721
-0,721
-0,721
-0,718
-0,718
-0,72
-0,72
-0,72
-0,721
-0,72
-0,72
-0,72
-0,718
-0,72
-0,72
-0,717
-0,72
-0,718
-0,721
-0,718
-0,721
-0,72
-0,72
-0,718
-0,718
-0,718
-0,718
-0,717
-0,718
-0,718
-0,717
-0,717
-0,718
-0,718
-0,717
-0,715
-0,717
-0,717
-0,718
-0,717
-0,717
-0,717
-0,715
-0,717
-0,717
-0,717
-0,717
-0,717
-0,715
-0,718
-0,715
-0,715
-0,715
-0,717
-0,715
-0,715
-0,715
-0,715
-0,715
-0,715
-0,715
-0,714
-0,714
-0,717
-0,714
-0,715
-0,714
-0,714
-0,715
-0,714
-0,715
-0,714
-0,714
-0,712
-0,712
-0,714
-0,712
-0,714
-0,712
-0,712
-0,712
-0,714
-0,712
-0,714
-0,712
-0,712
-0,712
-0,712
-0,712
-0,712
-0,712
-0,711
-0,711
-0,712
-0,712
-0,711
-0,711
-0,711
-0,711
-0,709
-0,711
-0,709
-0,709
-0,709
-0,709
-0,711
-0,711
-0,711
-0,709
-0,709
-0,711
-0,709
-0,709
-0,709
-0,708
-0,709
-0,708
-0,709
-0,709
-0,709
-0,709
-0,708
-0,708
-0,709
-0,708
-0,709
-0,708
-0,708
-0,708
-0,708
-0,708
-0,708
-0,708
-0,708
-0,709
-0,708
-0,708
-0,709
-0,708
-0,706
-0,706
-0,706
-0,708
-0,708
-0,705
-0,705
-0,706
-0,706
-0,706
-0,706
-0,708
-0,708
-0,706
-0,706
-0,705
-0,705
-0,708
-0,705
-0,706
-0,705
-0,705
-0,706
-0,706
-0,705
-0,706
-0,706
-0,706
-0,705
-0,705
-0,705
-0,705
-0,703
-0,703
-0,705
-0,705
-0,705
-0,705
-0,705
-0,705
-0,705
-0,705
-0,703
-0,705
-0,705
-0,703
-0,703
-0,703
-0,703
-0,703
-0,702
-0,703
-0,705
-0,703
-0,702
-0,702
-0,703
-0,703
-0,702
-0,7
-0,702
-0,703
-0,703
-0,703
-0,705
-0,702
-0,703
-0,703
-0,703
-0,703
-0,702
-0,702
-0,702
-0,702
-0,702
-0,7
-0,703
-0,7
-0,7
-0,7
-0,7
-0,7
-0,702
-0,702
-0,7
-0,7
-0,7
-0,7
-0,7
-0,7
-0,7
-0,7
-0,7
-0,702
-0,702
-0,699
-0,699
-0,7
-0,699
-0,702
-0,699
-0,7
-0,699
-0,699
-0,697
-0,699
-0,699
-0,7
-0,699
-0,7
-0,699
-0,702
-0,7
-0,699
-0,699
-0,699
-0,699
-0,697
-0,697
-0,699
-0,699
-0,699
-0,697
-0,7
-0,699
-0,699
-0,699
-0,699
-0,699
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,697
-0,696
-0,697
-0,696
-0,696
-0,696
-0,696
-0,696
-0,696
-0,694
-0,694
-0,696
-0,696
-0,696
-0,694
-0,694
-0,693
-0,694
-0,696
-0,694
-0,696
-0,696
-0,696
-0,694
-0,694
-0,694
-0,694
-0,693
-0,693
-0,694
-0,693
-0,694
-0,694
-0,694
-0,694
-0,694
-0,693
-0,694
-0,693
-0,694
-0,693
-0,693
-0,693
-0,693
-0,694
-0,693
-0,693
-0,694
-0,694
-0,693
-0,693
-0,694
-0,693
-0,693
-0,693
-0,693
-0,691
-0,693
-0,691
-0,691
-0,691
-0,691
-0,693
-0,693
-0,691
-0,693
-0,694
-0,693
-0,694
-0,693
-0,691
-0,693
-0,69
-0,69
-0,69
-0,691
-0,691
-0,69
-0,691
-0,691
-0,691
-0,691
-0,691
-0,693
-0,69
-0,69
-0,691
-0,691
-0,691
-0,691
-0,691
-0,691
-0,691
-0,69
-0,691
-0,691
-0,69
-0,691
-0,69
-0,69
-0,69
-0,69
-0,69
-0,69
-0,691
-0,69
-0,69
-0,69
-0,69
-0,69
-0,688
-0,688
-0,69
-0,688
-0,69
-0,688
-0,688
-0,688
-0,688
-0,688
-0,688
-0,688
-0,69
-0,69
-0,69
-0,688
-0,688
-0,688
-0,688
-0,69
-0,688
-0,687
-0,688
-0,688
-0,688
-0,688
-0,688
-0,688
-0,69
-0,688
-0,688
-0,687
-0,688
-0,687
-0,687
-0,687
-0,687
-0,687
-0,687
-0,687
-0,688
-0,687
-0,687
-0,687
-0,687
-0,688
-0,687
-0,687
-0,687
-0,685
-0,685
-0,687
-0,687
-0,688
-0,687
-0,688
-0,687
-0,687
-0,687
-0,687
-0,687
-0,687
-0,685
-0,687
-0,687
-0,687
-0,687
-0,687
-0,685
-0,687
-0,687
-0,685
-0,687
-0,685
-0,687
-0,687
-0,685
-0,685
-0,685
-0,687
-0,685
-0,685
-0,685
-0,685
-0,685
-0,685
-0,685
-0,685
-0,684
-0,685
-0,684
-0,685
-0,684
-0,684
-0,684
-0,685
-0,684
-0,684
-0,684
-0,684
-0,685
-0,684
-0,684
-0,682
-0,682
-0,684
-0,682
-0,682
-0,684
-0,682
-0,682
-0,684
-0,684
-0,684
-0,684
-0,682
-0,682
-0,68
-0,682
-0,682
-0,682
-0,682
-0,682
-0,682
-0,682
-0,685
-0,682
-0,682
-0,682
-0,682
-0,68
-0,682
-0,68
-0,682
-0,682
-0,682
-0,682
-0,68
-0,682
-0,684
-0,682
-0,682
-0,682
-0,682
-0,68
-0,68
-0,68
-0,682
-0,68
-0,679
-0,68
-0,68
-0,68
-0,679
-0,68
-0,68
-0,68
-0,68
-0,68
-0,682
-0,68
-0,679
-0,682
-0,68
-0,68
-0,68
-0,682
-0,68
-0,68
-0,68
-0,68
-0,682
-0,68
-0,677
-0,68
-0,682
-0,679
-0,679
-0,68
-0,679
-0,679
-0,68
-0,68
-0,68
-0,679
-0,679
-0,679
-0,679
-0,68
-0,68
-0,679
-0,679
-0,679
-0,68
-0,679
-0,679
-0,677
-0,679
-0,679
-0,679
-0,679
-0,679
-0,679
-0,679
-0,677
-0,679
-0,679
-0,677
-0,676
-0,679
-0,677
-0,677
-0,677
-0,679
-0,679
-0,677
-0,677
-0,677
-0,677
-0,676
-0,677
-0,677
-0,676
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,677
-0,679
-0,676
-0,676
-0,676
-0,676
-0,677
-0,676
-0,676
-0,676
-0,674
-0,677
-0,677
-0,676
-0,676
-0,679
-0,676
-0,676
-0,677
-0,676
-0,676
-0,677
-0,676
-0,677
-0,677
-0,676
-0,674
-0,676
-0,676
-0,676
-0,676
-0,676
-0,676
-0,676
-0,676
-0,676
-0,676
-0,674
-0,676
-0,676
-0,676
-0,676
-0,674
-0,674
-0,676
-0,676
-0,674
-0,674
-0,673
-0,671
-0,673
-0,674
-0,674
-0,674
-0,673
-0,674
-0,674
-0,674
-0,673
-0,674
-0,674
-0,673
-0,674
-0,673
-0,673
-0,673
-0,673
-0,674
-0,674
-0,673
-0,674
-0,674
-0,673
-0,673
-0,674
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,674
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,673
-0,671
-0,673
-0,67
-0,671
-0,671
-0,673
-0,671
-0,671
-0,673
-0,673
-0,671
-0,671
-0,671
-0,671
-0,671
-0,67
-0,673
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,67
-0,671
-0,67
-0,671
-0,671
-0,67
-0,67
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,671
-0,67
-0,671
-0,671
-0,671
-0,671
-0,671
-0,673
-0,671
-0,67
-0,67
-0,67
-0,671
-0,67
-0,67
-0,67
-0,671
-0,67
-0,67
-0,671
-0,67
-0,671
Прошу прощения что не в файле. Почему то не получилось прикрепить *.txt.

Сообщение отредактировано: Вованчик - 17.12.09, 08:56

Ну ЭТО больше похоже на логарифмическую.....

...или функция аппроксимации предопределена???

Здесь уравнение Вагнера(не композитор)почти сказочно ложится на эту кучу....
Прикреплённый файлВованчик.rar (37.84 Кбайт, скачиваний: 241)

вообще необходимый мне процесс сравнивают с разрядом конденсатора, поэтому функцией выбрали экспоненту.
и результат расчета по ссылке http://twtmas.mpei.ac.ru/mas/worksheets/Fit_f_x_a_b_c.mcd с вводом экспоненциальной функции дал очень хороший результат. Пытаюсь сейчас сделать картинку как это выглядит, но сервер глючит. Как только получиться выложу.

и еще - точки которые я выложил можно сказать идеальный вариант сигнала. бывает и хуже - например см. файл.

Прикреплённая картинка

Другая экспоненциальная....

Y=a+exp(b/X) + C

... и тогда почти похоже на правду...

for i := 1 to Nuz do
begin
SumX := SumX + 1/X[i];
SumY := SumY + ln(Y[i]);
SumSqrX := SumSqrX + Sqr(1/X[i]);
SumXY := SumXY + 1/X[i]*ln(Y[i]);
end;

b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX));
a := (SumY-b*SumX)/Nuz;
b1 := b;
a1 := exp(a);

Y_calc := a1*exp(b1/X);
Прикреплённый файлВованчик.rar (45.96 Кбайт, скачиваний: 263)

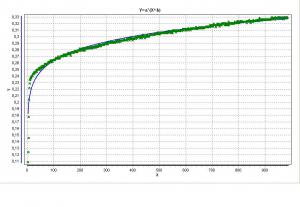
Степенная Y=a*(X^b)



for i := 1 to Nuz do
begin
SumX := SumX + log10(X[i]);
SumY := SumY + log10(Y[i]);
SumSqrX := SumSqrX + Sqr(log10(X[i]));
SumXY := SumXY + log10(X[i])*log10(Y[i]);
end;

b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX));
a := (SumY-b*SumX)/Nuz;
b1 := b;
a1 := Power(10,a);

Y_calc := a1*Power(X,b1);

Прикреплённая картинка

за идею 1/X огромный респект...
попробовал разные исходные данные - вроде как все устраивает

а есть ли способы сделать аппроксимацию не линейной функцией?

Конечно есть...

а какой изволите???????

Цитата repz @ 17.12.09, 13:30

а какой изволите???????

вот в этом то весь и вопрос...

вот например касаясь моего вопроса ранее:
допустим один набор данных хорошо аппроксимируется функцией f(x)=a*exp(b*x), а второй f(x)=a*exp(b/x).
как поступать в таком случае? каким единым методом обрабатывать эти два набора чтобы получить что-нибудь реальное.

Сообщение отредактировано: Вованчик - 17.12.09, 13:38

А вот для этого существует целая "туча" методов оценки статистик...

Мелкие детали (и не очень) лучше черпать из литературы, например Кобзарь "Прикладная математическая статистика"

Для Вашего случая - определитесь с неоходимым набором функций. Их будет всего-то штук несколько, а если и много - ничего страшного.

Критерий оценки оптимальной - детерминация и остаточная дисперсия (в самом босятском раскладе). Если у Вас это диссертация или научный труд - придется отнестись к делу серьезно и тему освоить... (и не доводить дело до заноса тяжелых хвостов)

Ну а по босятски - где детерминация ближе к единице, а остаточная дисперсия стремится к нулю - та функция и Ваша. Алгоритм реализации проще выкройки семейных трусов...

Цитата

Для Вашего случая - определитесь с неоходимым набором функций. Их будет всего-то штук несколько, а если и много - ничего страшного.

Критерий оценки оптимальной - детерминация и остаточная дисперсия (в самом босятском раскладе). Если у Вас это диссертация или научный труд - придется отнестись к делу серьезно и тему освоить... (и не доводить дело до заноса тяжелых хвостов)

Ну а по босятски - где детерминация ближе к единице, а остаточная дисперсия стремится к нулю - та функция и Ваша. Алгоритм реализации проще выкройки семейных трусов...

Спасибо за советы. Это у меня не диссертация и не научный труд - мне необходимо обработать данные на переносном приборе который снимает показания с датчиков. Попробую что получиться с детерминацией и остаточной дисперсией.

Наткнулся на этом форуме, что для нахождения трех неизвестных в экспоненциальной функции можно использовать Метод Левенберга-Марквардта или схему Брауна. Есть ли смысл покопаться в этом направлении?

Копаться всегда имеет смысл.. (кроме как в том,что не тонет)

хотя для экспоненциальных данного вида этими методами ничего не выйдет.
Здесь константа "С" не связывает зависимые переменные с объясняющими.

Вопрос, почему именно экспоненциальные, если в вашем случае это не установка преподавателя... (или заказчик так хочет)

В подобных случаях все же нужно плясать от физической сути процессов, а не пользовать формальные описания...или хотя бы выделять
формальные (безразмерные критерии) и описывать процессы в критериальных уравнениях...

Цитата repz @ 17.12.09, 19:46

Вопрос, почему именно экспоненциальные, если в вашем случае это не установка преподавателя... (или заказчик так хочет)

есть некоторые теоретические выкладки в которых есть ссылка на экспоненциальную зависимость...

... ну раз только экпоненциально - тогда...

Y = EXP( A0 + A1/X + A2*(1/X)^-1.5 + A3*(1/X)^-2 + A4*(1/X)^-2.5 + A5*(1/X)^-3 ) - 1

Сообщение отредактировано: repz - 19.12.09, 17:32

Прикреплённая картинка

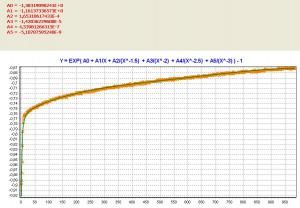
Я правильно понимаю что решить это уравнение можно например с помощью
аппроксимации произвольным набором базисных функций описанным
здесь?

Цитата

Y = EXP( A0 + A1/X + A2*(1/X)^-1.5 + A3*(1/X)^-2 + A4*(1/X)^-2.5 + A5*(1/X)^-3 ) - 1

И как выбрать оптимально количество коэффициентов для этой функции (можно написать и 10 и 20)?

Сообщение отредактировано: Вованчик - 22.12.09, 13:32

Спасибо за код.
...Я уже сделал аппроксимацию произвольным набором базисных функций.

Еще один вопросик: как можно решить вот такое уравнение:
Y(X) = A0 * EXP(B0 * X) + A1 * EXP(B1 * X)

Y(X) = A0 * EXP(B0 * X) + A1 * EXP(B1 * X)

Y(X) = Y0(X) + Y1(X)
Y0(X) = A0 * EXP(B0 * X)
Y1(X) = A1 * EXP(B1 * X)

Бесконечное (и бессмысленное) множество равноценных решений, эквивалентных Y(X) = A * EXP(B * X)

Друзья, добрый день.
Хоть прошло уже немало лет, решил поднять тему, т.к. ближе темы к моему вопросу не нашел.
Стоит задача аппроксимировать экспериментальные данные функцией y(t)=a+b*(1-exp(-c*t))+d*t
В случае просто экспотенциальной функции все более-менее понятно как быть, а вот как правильно выполнить аппроксимацию, когда функция такой сложности - неясно. И есть ли вообще аналитическое решение по такого рода функции, или необходимо использовать методы перебора параметров?
Спасибо.

Если исходных данных ровно 4, то решаете СЛАУ.
Если меньше, то навешивайте нравящееся вам ограничение/условие.
Если больше, то МНК, и в путь.

Исходных данных несколько тысяч точек. Загвоздка как раз в том, что я не знаю, как функцию такого вида аппроксимировать с помощью МНК. Была бы просто экспонента, то все ясно, прологарифмиров привели к линейному виду и вперед. А здесь как быть? Тут помимо экспоненты еще линейная составляющая есть, да перед экспонентой еще единица эта... Моих знаний в математике не хватает.

Экспонента блестяще раскладывается в ряд, поэтому делайте:
1. Многочлен нужной (удобоваримой) степени, и приближайте исходную задачу чрез подстановку вместо экспоненты многочлена методом МНК.
2. Получив многочлен, подберёте/вычислите нужное 'c'.

Спасибо Вам за ответ. Буду пробовать разложить экспоненту в ряд Маклорена.

Нет, не надо раскладывать экспоненту!!!
Надо лишь:
1. заменить её многочленом какой-нибудь степени;
2. решить вашу задачу без экспоненты, но с многочленом;
3. подобрать число для той экспоненты по коэффициентам многочлена, полученного из п. 2.

Вы это имели ввиду?
exp(x) = 1+ x/1! + x^2/2! + ... + x^n/n! + ...

Цитата nostromo @ 16.04.22, 15:00

Стоит задача аппроксимировать экспериментальные данные функцией y(t)=a+b*(1-exp(-c*t))+d*t

Вообще-то это y(t) = k₁ + k₂ * exp(k₃ * t) + k₄ * t. Зачем усложнять ненужными константами?

nostromo, когда-то давно подобные задачки решал методом Ньютона.
Определялись параметры вольт-амперной характеристики p-n перехода.
Только там было 1-2 экспоненты и до 6 параметров.

Цитата Akina @ 16.04.22, 20:10

Вообще-то это y(t) = k₁ + k₂ * exp(k₃ * t) + k₄ * t. Зачем усложнять ненужными константами?

Akina, преобразовать функцию к этому виду несложно. У меня нет понимания, как функцию такого рода (когда помимо экспоненты и k₁ присутствует еще k₄*t) правильно аппроксимировать МНК. Примеров я не нашел, поэтому и попросил помочь, если кто знает.
Славян предложил (ему отдельное спасибо) разложить экспоненту в степенной ряд. После разложения и приведения подобных слагаемых можно получить полином n-степени и далее уже решить задачу с помощью МНК. Если кто знает как это сделать проще, не прибегая к разложению, подскажите пожалуйста.

Да сколько раз говорить! Не надо раскладывать экспоненту!! Надо приблизить всё многочленом, преобразовать многочлен к нужному вам виду с экспонентой, а потом приблизить экспоненту по имеющемуся многочлену.

Я очень сильно извиняюсь, но я тогда не пойму, что значит приблизить все многочленом…

Пример: надо приблизить вашу задачу функцией exp(k*x) + s*x на отрезке [p,q].
Приближаем "многочленом" третьей степени: a + b*x + c*x² + d*x³. Имеем: 2 + 3*x - 4*x³.
Далее, подставляем: exp(k*x) + s*x -> (2 - 4*x³) + 3*x. s уже есть, равно 3. Нужно=осталось приблизить exp(k*x) многочленом 2 - 4*x³. МНК, аналитически беря интеграл, и находим k.

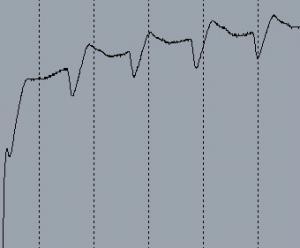
Добрый день всем.
Снова прошу вашей помощи. Результат эксперимента я аппроксимировал, но теперь заказчик требует на графике построить доверительный интервал, как на рисунке (изображен пунктирными линиями выше/ниже основного аппроксимированного графика). Почитал в Интернете, вообще ничего похожего не нашел, как правильно делать. Просто как этот интервал вычислить, более-менее понял, а вот как еще такие графики построить...
Может кто решал с подобную задачу, подскажите пожалуйста.
Спасибо.

Прикреплённая картинка

nostromo
Ну тут разве что остаётся предложить взять в руки учебник по статистическому анализу.
Сорри, если получилось обидно.