аппроксимация экспонентой f(x)=a*exp(b*x)+c
аппроксимация экспонентой f(x)=a*exp(b*x)+c
 |
Наши проекты:
Журнал · Discuz!ML · Wiki · DRKB · Помощь проекту |
|
| ПРАВИЛА | FAQ | Помощь | Поиск | Участники | Календарь | Избранное | RSS |
| [3.142.197.212] |

|
|
 правила раздела Алгоритмы
правила раздела Алгоритмы
1. Помните, что название темы должно хоть как-то отражать ее содержимое (не создавайте темы с заголовком ПОМОГИТЕ, HELP и т.д.). Злоупотребление заглавными буквами в заголовках тем ЗАПРЕЩЕНО.
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code.../code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии "срочно надо", заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code.../code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии "срочно надо", заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке

Модераторы: Akina, shadeofgray
| Страницы: (3) 1 [2] 3 все ( Перейти к последнему сообщению ) |
 аппроксимация экспонентой f(x)=a*exp(b*x)+c
аппроксимация экспонентой f(x)=a*exp(b*x)+c
|
Сообщ.
#16
,
|
|
|
|
Цитата Для Вашего случая - определитесь с неоходимым набором функций. Их будет всего-то штук несколько, а если и много - ничего страшного. Критерий оценки оптимальной - детерминация и остаточная дисперсия (в самом босятском раскладе). Если у Вас это диссертация или научный труд - придется отнестись к делу серьезно и тему освоить... (и не доводить дело до заноса тяжелых хвостов) Ну а по босятски - где детерминация ближе к единице, а остаточная дисперсия стремится к нулю - та функция и Ваша. Алгоритм реализации проще выкройки семейных трусов... Спасибо за советы. Это у меня не диссертация и не научный труд - мне необходимо обработать данные на переносном приборе который снимает показания с датчиков. Попробую что получиться с детерминацией и остаточной дисперсией. Наткнулся на этом форуме, что для нахождения трех неизвестных в экспоненциальной функции можно использовать Метод Левенберга-Марквардта или схему Брауна. Есть ли смысл покопаться в этом направлении? |
|
Сообщ.
#17
,
|
|
|
|
Копаться всегда имеет смысл.. (кроме как в том,что не тонет)
хотя для экспоненциальных данного вида этими методами ничего не выйдет. Здесь константа "С" не связывает зависимые переменные с объясняющими. Вопрос, почему именно экспоненциальные, если в вашем случае это не установка преподавателя... (или заказчик так хочет) В подобных случаях все же нужно плясать от физической сути процессов, а не пользовать формальные описания...или хотя бы выделять формальные (безразмерные критерии) и описывать процессы в критериальных уравнениях... |
|
Сообщ.
#18
,
|
|
|
|
Цитата repz @ Вопрос, почему именно экспоненциальные, если в вашем случае это не установка преподавателя... (или заказчик так хочет) есть некоторые теоретические выкладки в которых есть ссылка на экспоненциальную зависимость... |
|
Сообщ.
#19
,
|
|
|
|
|
Сообщ.
#20
,
|
|
|
|
Я правильно понимаю что решить это уравнение можно например с помощью
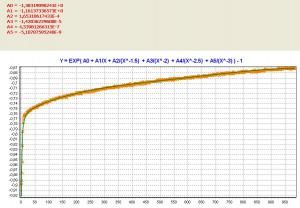
аппроксимации произвольным набором базисных функций описанным здесь? Цитата Y = EXP( A0 + A1/X + A2*(1/X)^-1.5 + A3*(1/X)^-2 + A4*(1/X)^-2.5 + A5*(1/X)^-3 ) - 1 И как выбрать оптимально количество коэффициентов для этой функции (можно написать и 10 и 20)? |
|
Сообщ.
#21
,
|
|
|
|
Спасибо за код.
...Я уже сделал аппроксимацию произвольным набором базисных функций. Еще один вопросик: как можно решить вот такое уравнение: Y(X) = A0 * EXP(B0 * X) + A1 * EXP(B1 * X) |
|
Сообщ.
#22
,
|
|
|
|
Y(X) = A0 * EXP(B0 * X) + A1 * EXP(B1 * X)
Y(X) = Y0(X) + Y1(X) Y0(X) = A0 * EXP(B0 * X) Y1(X) = A1 * EXP(B1 * X) Бесконечное (и бессмысленное) множество равноценных решений, эквивалентных Y(X) = A * EXP(B * X) |
|
Сообщ.
#23
,
|
|
|
|
Друзья, добрый день.
Хоть прошло уже немало лет, решил поднять тему, т.к. ближе темы к моему вопросу не нашел. Стоит задача аппроксимировать экспериментальные данные функцией y(t)=a+b*(1-exp(-c*t))+d*t В случае просто экспотенциальной функции все более-менее понятно как быть, а вот как правильно выполнить аппроксимацию, когда функция такой сложности - неясно. И есть ли вообще аналитическое решение по такого рода функции, или необходимо использовать методы перебора параметров? Спасибо. |
|
Сообщ.
#24
,
|
|
|
|
Если исходных данных ровно 4, то решаете СЛАУ.
Если меньше, то навешивайте нравящееся вам ограничение/условие. Если больше, то МНК, и в путь. |
|
Сообщ.
#25
,
|
|
|
|
Исходных данных несколько тысяч точек. Загвоздка как раз в том, что я не знаю, как функцию такого вида аппроксимировать с помощью МНК.
 Была бы просто экспонента, то все ясно, прологарифмиров привели к линейному виду и вперед. А здесь как быть? Тут помимо экспоненты еще линейная составляющая есть, да перед экспонентой еще единица эта... Моих знаний в математике не хватает. Была бы просто экспонента, то все ясно, прологарифмиров привели к линейному виду и вперед. А здесь как быть? Тут помимо экспоненты еще линейная составляющая есть, да перед экспонентой еще единица эта... Моих знаний в математике не хватает. |
|
Сообщ.
#26
,
|
|
|
|
Экспонента блестяще раскладывается в ряд, поэтому делайте:
1. Многочлен нужной (удобоваримой) степени, и приближайте исходную задачу чрез подстановку вместо экспоненты многочлена методом МНК. 2. Получив многочлен, подберёте/вычислите нужное 'c'. |
|
Сообщ.
#27
,
|
|
|
|
Спасибо Вам за ответ. Буду пробовать разложить экспоненту в ряд Маклорена.
|
|
Сообщ.
#28
,
|
|
|
|
Нет, не надо раскладывать экспоненту!!!
 Надо лишь: 1. заменить её многочленом какой-нибудь степени; 2. решить вашу задачу без экспоненты, но с многочленом; 3. подобрать число для той экспоненты по коэффициентам многочлена, полученного из п. 2. |
|
Сообщ.
#29
,
|
|
|
|
Вы это имели ввиду?
exp(x) = 1+ x/1! + x^2/2! + ... + x^n/n! + ... |
|
Сообщ.
#30
,
|
|
|
|
Цитата nostromo @ Стоит задача аппроксимировать экспериментальные данные функцией y(t)=a+b*(1-exp(-c*t))+d*t Вообще-то это y(t) = k1 + k2 * exp(k3 * t) + k4 * t. Зачем усложнять ненужными константами? |
1 пользователей читают эту тему (1 гостей и 0 скрытых пользователей)
0 пользователей:
[ Script execution time: 0,0582 ] [ 14 queries used ] [ Generated: 27.07.24, 13:53 GMT ]