аппроксимация экспонентой f(x)=a*exp(b*x)+c
аппроксимация экспонентой f(x)=a*exp(b*x)+c
 |
Наши проекты:
Журнал · Discuz!ML · Wiki · DRKB · Помощь проекту |
|
| ПРАВИЛА | FAQ | Помощь | Поиск | Участники | Календарь | Избранное | RSS |
| [3.135.216.75] |

|
|
 правила раздела Алгоритмы
правила раздела Алгоритмы
1. Помните, что название темы должно хоть как-то отражать ее содержимое (не создавайте темы с заголовком ПОМОГИТЕ, HELP и т.д.). Злоупотребление заглавными буквами в заголовках тем ЗАПРЕЩЕНО.
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code.../code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии "срочно надо", заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code.../code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии "срочно надо", заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке

Модераторы: Akina, shadeofgray
| Страницы: (3) [1] 2 3 все ( Перейти к последнему сообщению ) |
 аппроксимация экспонентой f(x)=a*exp(b*x)+c
аппроксимация экспонентой f(x)=a*exp(b*x)+c
|
Сообщ.
#1
,
|
|
|
|
Здравствуйте.
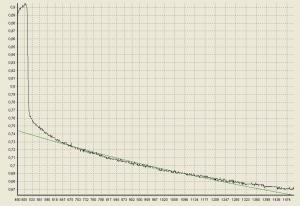
Подскажите пожалуйста каким способом лучше всего произвести аппроксимацию данных экспонентой f(x)=a*exp(b*x)+c. Исходные данные: набор из 1000 точек с интервалом 50мкс. Пробовал ввести данные по ссылке http://twtmas.mpei.ac.ru/mas/worksheets/Fit_f_x_a_b_c.mcd). Брал не все точки, а только 20 с равным интервалом - получилось красиво. Но какой метод там используется так и не нашел. Спасибо. |
|
Сообщ.
#2
,
|
|
|
|
SumX := 0;
SumY := 0; SumSqrX := 0; SumXY := 0; for i := 1 to Nuz do //до число узлов (точек) begin SumX := SumX + X[i]; SumY := SumY + ln(Y[i]); SumSqrX := SumSqrX + Sqr(X[i]); SumXY := SumXY + X[i]*ln(Y[i]); end; b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX)); a := (SumY-b*SumX)/Nuz; b1 := b; a1 := exp(a); Y_calc := a1*exp(b1*X);//интерполяция Просто линеаризация Если коэфф "С" для Вас критично - задавайтесь им предварительно, и вместо y[i] будет y[i]-c или плюс (сами разберетесь...) |
|
Сообщ.
#3
,
|
|
|
|
|
Сообщ.
#4
,
|
|
|
|
Линеаризация - это не аппроксимация линейной функцией
Выложите свои "Точки" (таблично), посмотрим что получается... |
|
Сообщ.
#5
,
|
|
|
|
Цитата Линеаризация - это не аппроксимация линейной функцией Это все понятно. Пробовал сделать аппроксимацию функцией f(x)=a*exp(b*x)+c. Коэффициент с принял за константу, перенес влево, логарифмировал и т.д. и т.п. Тоже самое что вы предлагали. Ваш код и мой дали один и тот же результат (что в принципе логично). Точки (шаг по X равный): -0,897 -0,891 -0,876 -0,854 -0,822 -0,795 -0,778 -0,771 -0,766 -0,765 -0,763 -0,762 -0,762 -0,763 -0,76 -0,76 -0,76 -0,76 -0,76 -0,757 -0,757 -0,757 -0,756 -0,754 -0,756 -0,754 -0,754 -0,754 -0,754 -0,753 -0,753 -0,753 -0,751 -0,753 -0,751 -0,75 -0,75 -0,75 -0,75 -0,75 -0,75 -0,75 -0,748 -0,748 -0,748 -0,75 -0,748 -0,747 -0,748 -0,748 -0,745 -0,747 -0,747 -0,747 -0,747 -0,747 -0,744 -0,745 -0,747 -0,744 -0,744 -0,744 -0,744 -0,744 -0,742 -0,742 -0,741 -0,742 -0,742 -0,741 -0,741 -0,742 -0,741 -0,741 -0,741 -0,741 -0,739 -0,739 -0,739 -0,738 -0,739 -0,739 -0,738 -0,738 -0,738 -0,738 -0,736 -0,736 -0,739 -0,738 -0,736 -0,736 -0,738 -0,736 -0,736 -0,736 -0,736 -0,735 -0,735 -0,735 -0,735 -0,735 -0,735 -0,735 -0,733 -0,733 -0,733 -0,733 -0,732 -0,733 -0,732 -0,733 -0,733 -0,733 -0,733 -0,73 -0,732 -0,732 -0,733 -0,733 -0,732 -0,732 -0,73 -0,73 -0,73 -0,73 -0,73 -0,729 -0,729 -0,729 -0,729 -0,73 -0,729 -0,729 -0,729 -0,727 -0,729 -0,729 -0,729 -0,727 -0,727 -0,729 -0,729 -0,729 -0,729 -0,729 -0,729 -0,727 -0,727 -0,727 -0,726 -0,726 -0,726 -0,727 -0,724 -0,726 -0,726 -0,726 -0,726 -0,726 -0,726 -0,726 -0,724 -0,729 -0,724 -0,724 -0,724 -0,723 -0,724 -0,724 -0,724 -0,724 -0,724 -0,724 -0,723 -0,723 -0,723 -0,723 -0,723 -0,721 -0,723 -0,723 -0,723 -0,723 -0,723 -0,723 -0,721 -0,721 -0,723 -0,721 -0,721 -0,721 -0,721 -0,721 -0,721 -0,721 -0,721 -0,718 -0,718 -0,72 -0,72 -0,72 -0,721 -0,72 -0,72 -0,72 -0,718 -0,72 -0,72 -0,717 -0,72 -0,718 -0,721 -0,718 -0,721 -0,72 -0,72 -0,718 -0,718 -0,718 -0,718 -0,717 -0,718 -0,718 -0,717 -0,717 -0,718 -0,718 -0,717 -0,715 -0,717 -0,717 -0,718 -0,717 -0,717 -0,717 -0,715 -0,717 -0,717 -0,717 -0,717 -0,717 -0,715 -0,718 -0,715 -0,715 -0,715 -0,717 -0,715 -0,715 -0,715 -0,715 -0,715 -0,715 -0,715 -0,714 -0,714 -0,717 -0,714 -0,715 -0,714 -0,714 -0,715 -0,714 -0,715 -0,714 -0,714 -0,712 -0,712 -0,714 -0,712 -0,714 -0,712 -0,712 -0,712 -0,714 -0,712 -0,714 -0,712 -0,712 -0,712 -0,712 -0,712 -0,712 -0,712 -0,711 -0,711 -0,712 -0,712 -0,711 -0,711 -0,711 -0,711 -0,709 -0,711 -0,709 -0,709 -0,709 -0,709 -0,711 -0,711 -0,711 -0,709 -0,709 -0,711 -0,709 -0,709 -0,709 -0,708 -0,709 -0,708 -0,709 -0,709 -0,709 -0,709 -0,708 -0,708 -0,709 -0,708 -0,709 -0,708 -0,708 -0,708 -0,708 -0,708 -0,708 -0,708 -0,708 -0,709 -0,708 -0,708 -0,709 -0,708 -0,706 -0,706 -0,706 -0,708 -0,708 -0,705 -0,705 -0,706 -0,706 -0,706 -0,706 -0,708 -0,708 -0,706 -0,706 -0,705 -0,705 -0,708 -0,705 -0,706 -0,705 -0,705 -0,706 -0,706 -0,705 -0,706 -0,706 -0,706 -0,705 -0,705 -0,705 -0,705 -0,703 -0,703 -0,705 -0,705 -0,705 -0,705 -0,705 -0,705 -0,705 -0,705 -0,703 -0,705 -0,705 -0,703 -0,703 -0,703 -0,703 -0,703 -0,702 -0,703 -0,705 -0,703 -0,702 -0,702 -0,703 -0,703 -0,702 -0,7 -0,702 -0,703 -0,703 -0,703 -0,705 -0,702 -0,703 -0,703 -0,703 -0,703 -0,702 -0,702 -0,702 -0,702 -0,702 -0,7 -0,703 -0,7 -0,7 -0,7 -0,7 -0,7 -0,702 -0,702 -0,7 -0,7 -0,7 -0,7 -0,7 -0,7 -0,7 -0,7 -0,7 -0,702 -0,702 -0,699 -0,699 -0,7 -0,699 -0,702 -0,699 -0,7 -0,699 -0,699 -0,697 -0,699 -0,699 -0,7 -0,699 -0,7 -0,699 -0,702 -0,7 -0,699 -0,699 -0,699 -0,699 -0,697 -0,697 -0,699 -0,699 -0,699 -0,697 -0,7 -0,699 -0,699 -0,699 -0,699 -0,699 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,697 -0,696 -0,697 -0,696 -0,696 -0,696 -0,696 -0,696 -0,696 -0,694 -0,694 -0,696 -0,696 -0,696 -0,694 -0,694 -0,693 -0,694 -0,696 -0,694 -0,696 -0,696 -0,696 -0,694 -0,694 -0,694 -0,694 -0,693 -0,693 -0,694 -0,693 -0,694 -0,694 -0,694 -0,694 -0,694 -0,693 -0,694 -0,693 -0,694 -0,693 -0,693 -0,693 -0,693 -0,694 -0,693 -0,693 -0,694 -0,694 -0,693 -0,693 -0,694 -0,693 -0,693 -0,693 -0,693 -0,691 -0,693 -0,691 -0,691 -0,691 -0,691 -0,693 -0,693 -0,691 -0,693 -0,694 -0,693 -0,694 -0,693 -0,691 -0,693 -0,69 -0,69 -0,69 -0,691 -0,691 -0,69 -0,691 -0,691 -0,691 -0,691 -0,691 -0,693 -0,69 -0,69 -0,691 -0,691 -0,691 -0,691 -0,691 -0,691 -0,691 -0,69 -0,691 -0,691 -0,69 -0,691 -0,69 -0,69 -0,69 -0,69 -0,69 -0,69 -0,691 -0,69 -0,69 -0,69 -0,69 -0,69 -0,688 -0,688 -0,69 -0,688 -0,69 -0,688 -0,688 -0,688 -0,688 -0,688 -0,688 -0,688 -0,69 -0,69 -0,69 -0,688 -0,688 -0,688 -0,688 -0,69 -0,688 -0,687 -0,688 -0,688 -0,688 -0,688 -0,688 -0,688 -0,69 -0,688 -0,688 -0,687 -0,688 -0,687 -0,687 -0,687 -0,687 -0,687 -0,687 -0,687 -0,688 -0,687 -0,687 -0,687 -0,687 -0,688 -0,687 -0,687 -0,687 -0,685 -0,685 -0,687 -0,687 -0,688 -0,687 -0,688 -0,687 -0,687 -0,687 -0,687 -0,687 -0,687 -0,685 -0,687 -0,687 -0,687 -0,687 -0,687 -0,685 -0,687 -0,687 -0,685 -0,687 -0,685 -0,687 -0,687 -0,685 -0,685 -0,685 -0,687 -0,685 -0,685 -0,685 -0,685 -0,685 -0,685 -0,685 -0,685 -0,684 -0,685 -0,684 -0,685 -0,684 -0,684 -0,684 -0,685 -0,684 -0,684 -0,684 -0,684 -0,685 -0,684 -0,684 -0,682 -0,682 -0,684 -0,682 -0,682 -0,684 -0,682 -0,682 -0,684 -0,684 -0,684 -0,684 -0,682 -0,682 -0,68 -0,682 -0,682 -0,682 -0,682 -0,682 -0,682 -0,682 -0,685 -0,682 -0,682 -0,682 -0,682 -0,68 -0,682 -0,68 -0,682 -0,682 -0,682 -0,682 -0,68 -0,682 -0,684 -0,682 -0,682 -0,682 -0,682 -0,68 -0,68 -0,68 -0,682 -0,68 -0,679 -0,68 -0,68 -0,68 -0,679 -0,68 -0,68 -0,68 -0,68 -0,68 -0,682 -0,68 -0,679 -0,682 -0,68 -0,68 -0,68 -0,682 -0,68 -0,68 -0,68 -0,68 -0,682 -0,68 -0,677 -0,68 -0,682 -0,679 -0,679 -0,68 -0,679 -0,679 -0,68 -0,68 -0,68 -0,679 -0,679 -0,679 -0,679 -0,68 -0,68 -0,679 -0,679 -0,679 -0,68 -0,679 -0,679 -0,677 -0,679 -0,679 -0,679 -0,679 -0,679 -0,679 -0,679 -0,677 -0,679 -0,679 -0,677 -0,676 -0,679 -0,677 -0,677 -0,677 -0,679 -0,679 -0,677 -0,677 -0,677 -0,677 -0,676 -0,677 -0,677 -0,676 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,677 -0,679 -0,676 -0,676 -0,676 -0,676 -0,677 -0,676 -0,676 -0,676 -0,674 -0,677 -0,677 -0,676 -0,676 -0,679 -0,676 -0,676 -0,677 -0,676 -0,676 -0,677 -0,676 -0,677 -0,677 -0,676 -0,674 -0,676 -0,676 -0,676 -0,676 -0,676 -0,676 -0,676 -0,676 -0,676 -0,676 -0,674 -0,676 -0,676 -0,676 -0,676 -0,674 -0,674 -0,676 -0,676 -0,674 -0,674 -0,673 -0,671 -0,673 -0,674 -0,674 -0,674 -0,673 -0,674 -0,674 -0,674 -0,673 -0,674 -0,674 -0,673 -0,674 -0,673 -0,673 -0,673 -0,673 -0,674 -0,674 -0,673 -0,674 -0,674 -0,673 -0,673 -0,674 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,674 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,673 -0,671 -0,673 -0,67 -0,671 -0,671 -0,673 -0,671 -0,671 -0,673 -0,673 -0,671 -0,671 -0,671 -0,671 -0,671 -0,67 -0,673 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,67 -0,671 -0,67 -0,671 -0,671 -0,67 -0,67 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,671 -0,67 -0,671 -0,671 -0,671 -0,671 -0,671 -0,673 -0,671 -0,67 -0,67 -0,67 -0,671 -0,67 -0,67 -0,67 -0,671 -0,67 -0,67 -0,671 -0,67 -0,671 Прошу прощения что не в файле. Почему то не получилось прикрепить *.txt. |
|
Сообщ.
#6
,
|
|
|
|
Ну ЭТО больше похоже на логарифмическую.....
...или функция аппроксимации предопределена??? Здесь уравнение Вагнера(не композитор)почти сказочно ложится на эту кучу.... Прикреплённый файл  Вованчик.rar (37.84 Кбайт, скачиваний: 263) Вованчик.rar (37.84 Кбайт, скачиваний: 263)
|
|
Сообщ.
#7
,
|
|
|
|
вообще необходимый мне процесс сравнивают с разрядом конденсатора, поэтому функцией выбрали экспоненту.
и результат расчета по ссылке http://twtmas.mpei.ac.ru/mas/worksheets/Fit_f_x_a_b_c.mcd с вводом экспоненциальной функции дал очень хороший результат. Пытаюсь сейчас сделать картинку как это выглядит, но сервер глючит. Как только получиться выложу. |
|
Сообщ.
#8
,
|
|
|
|
|
Сообщ.
#9
,
|
|
|
|
Другая экспоненциальная....
Y=a+exp(b/X) + C ... и тогда почти похоже на правду... for i := 1 to Nuz do begin SumX := SumX + 1/X[i]; SumY := SumY + ln(Y[i]); SumSqrX := SumSqrX + Sqr(1/X[i]); SumXY := SumXY + 1/X[i]*ln(Y[i]); end; b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX)); a := (SumY-b*SumX)/Nuz; b1 := b; a1 := exp(a); Y_calc := a1*exp(b1/X); Прикреплённый файл  Вованчик.rar (45.96 Кбайт, скачиваний: 295) Вованчик.rar (45.96 Кбайт, скачиваний: 295)
|
|
Сообщ.
#10
,
|
|
|
|
Степенная Y=a*(X^b)
for i := 1 to Nuz do begin SumX := SumX + log10(X[i]); SumY := SumY + log10(Y[i]); SumSqrX := SumSqrX + Sqr(log10(X[i])); SumXY := SumXY + log10(X[i])*log10(Y[i]); end; b := (Nuz*SumXY-SumX*SumY)/(Nuz*SumSqrX-Sqr(SumX)); a := (SumY-b*SumX)/Nuz; b1 := b; a1 := Power(10,a); Y_calc := a1*Power(X,b1); Прикреплённая картинка
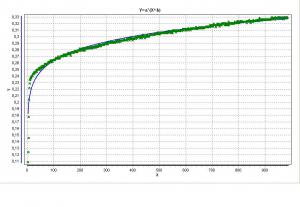
|
|
Сообщ.
#11
,
|
|
|
|
за идею 1/X огромный респект...
 попробовал разные исходные данные - вроде как все устраивает  |
|
Сообщ.
#12
,
|
|
|
|
а есть ли способы сделать аппроксимацию не линейной функцией?
|
|
Сообщ.
#13
,
|
|
|
|
Конечно есть...
а какой изволите??????? |
|
Сообщ.
#14
,
|
|
|
|
Цитата repz @ а какой изволите??????? вот в этом то весь и вопрос... вот например касаясь моего вопроса ранее: допустим один набор данных хорошо аппроксимируется функцией f(x)=a*exp(b*x), а второй f(x)=a*exp(b/x). как поступать в таком случае? каким единым методом обрабатывать эти два набора чтобы получить что-нибудь реальное. |
|
Сообщ.
#15
,
|
|
|
|
А вот для этого существует целая "туча" методов оценки статистик...
Мелкие детали (и не очень) лучше черпать из литературы, например Кобзарь "Прикладная математическая статистика" Для Вашего случая - определитесь с неоходимым набором функций. Их будет всего-то штук несколько, а если и много - ничего страшного. Критерий оценки оптимальной - детерминация и остаточная дисперсия (в самом босятском раскладе). Если у Вас это диссертация или научный труд - придется отнестись к делу серьезно и тему освоить... (и не доводить дело до заноса тяжелых хвостов) Ну а по босятски - где детерминация ближе к единице, а остаточная дисперсия стремится к нулю - та функция и Ваша. Алгоритм реализации проще выкройки семейных трусов... |
1 пользователей читают эту тему (1 гостей и 0 скрытых пользователей)
0 пользователей:
[ Script execution time: 0,0406 ] [ 14 queries used ] [ Generated: 6.10.24, 10:12 GMT ]